You know the log of 2 is .3010. Therefore you have:
dB = 10 x .3010
This time you have a gain so you use a plus sign to express the final result:
+3.01 dB or approximately +3 dB
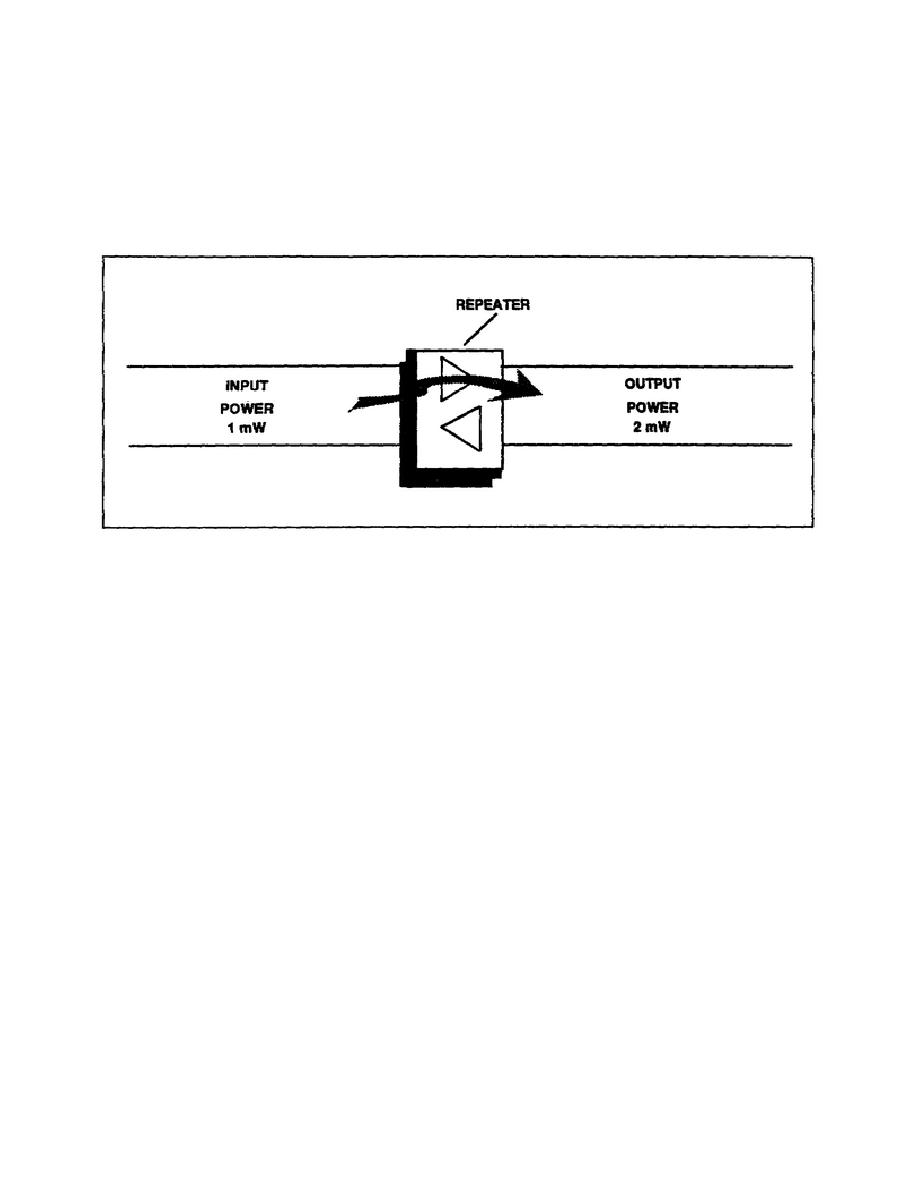
Figure 3-10. Repeater providing power gain.
b. In the first example, you had a power loss of 50 percent and this gave a loss of 3 dB. Then, in the
second example, you had a gain of twice as much power and this gave you a gain of 3 dB. This brings out two
important facts that you should remember:
(1) Loss of 3 dB always represents a 50-percent power loss. It doesn't matter how much power is
involved. When you lose half the power you always have a loss of 3 dB.
(2) A gain of 3 dB always represents a gain of twice as much power. Again the amount of power
involved doesn't matter. Whenever you gain twice as much power, you have a gain of 3 dB.
c. Seeing how formulas for dB loss and gain are solved has given you an idea of how decibels express the
power ratio in a circuit. There is no need to go into any further computations. Instead, the formulas have been
worked out for several common dB losses and gains. The results of these computations are given in Table 3-4.
6. You can find out how much power is lost or gained if you know the number of decibels lost or gained. Or
you can find out the number of decibels lost or gained when you know the amount of power lost or gained. To
show you how to use Table 3-4, here are a few examples.
a. Example 1. Suppose you have a circuit like that shown in Figure 3-11. The input power is .001 watt
and the output power is .000001 watt. The input power is
SS0031
3-32




 Previous Page
Previous Page
