the segment. In this case, you add 32.5% and 25%, which equals 57.5%.
Continue plotting using the same procedure:
32.5%
+ 25.0% = 57.5%
(the
end
of
the
second segment)
57.5%
+ 20.0% = 77.5%
(the
end
of
the
third segment)
77.5%
+ 15.0% = 92.5%
(the
end
of
the
fourth segment)
92.5%
+ 7.5% = 100.0%
(the
end
of
the
fifth segment)
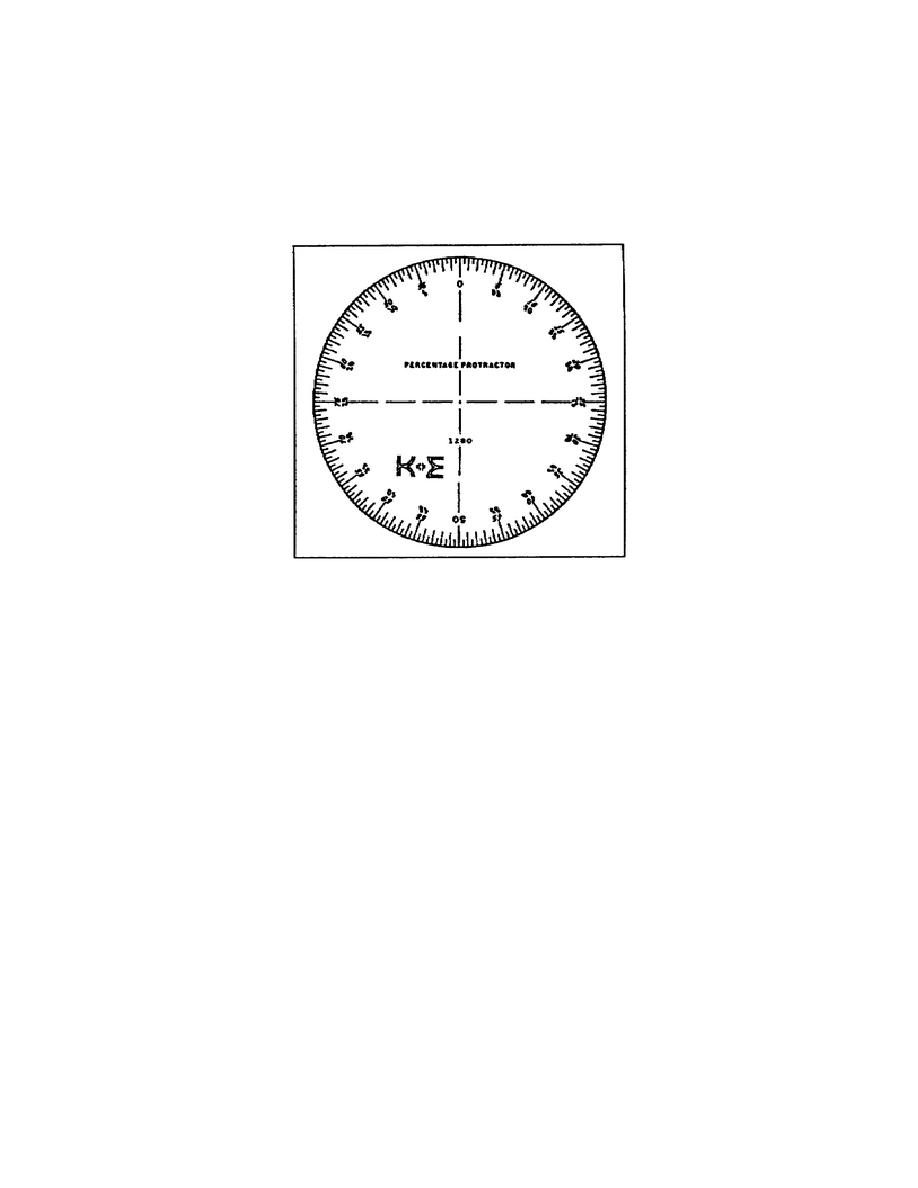
Figure 1-31.
Percentage protractor
Before proceeding with the lesson, take a moment and review the plotting
procedure used with a percentage protractor. You placed the "0" percent
graduation at the 12 o'clock position (which placed the 50% graduation at
the 6 o'clock position). You plotted the largest segment first, moving
clockwise.
The end of the first segment served as the start for the
second segment and so on.
You plot the segments largest to smallest
moving clockwise. The proof that you plotted correctly was that the last
or smallest segment ended at the "0" percent graduation. You used 100%
of the circle in your pie chart. If the last segment did not end at the
"0" percent graduation, you made a mistake, and you must recheck your
work.
(c) Plotting segments with a standard protractor. To plot the
segments using a standard protractor, you must determine the number of
degrees each segment uses.
Before you can determine the number of
degrees each segment uses, you must determine how many degrees of the
circle makeup 1% of the circle.
If you divide the total number of
degrees in a circle
1-37
SS0530




 Previous Page
Previous Page
