Learning Event 4:
EXPLAIN HOW COMBINATIONS OF GATES CAN CHANGE FUNCTIONS
1.
Logic systems can be designed many different ways to produce a specific result. The circuit
arrangement selected usually depends on the equipment designer. There is seldom a "best" way of
designing any binary system. Your job as a technician is to analyze and understand systems that already
exist, not to design systems. Very often, however, you will find that a careful analysis of a system or
partial system is the only way to prove its true operation.
2.
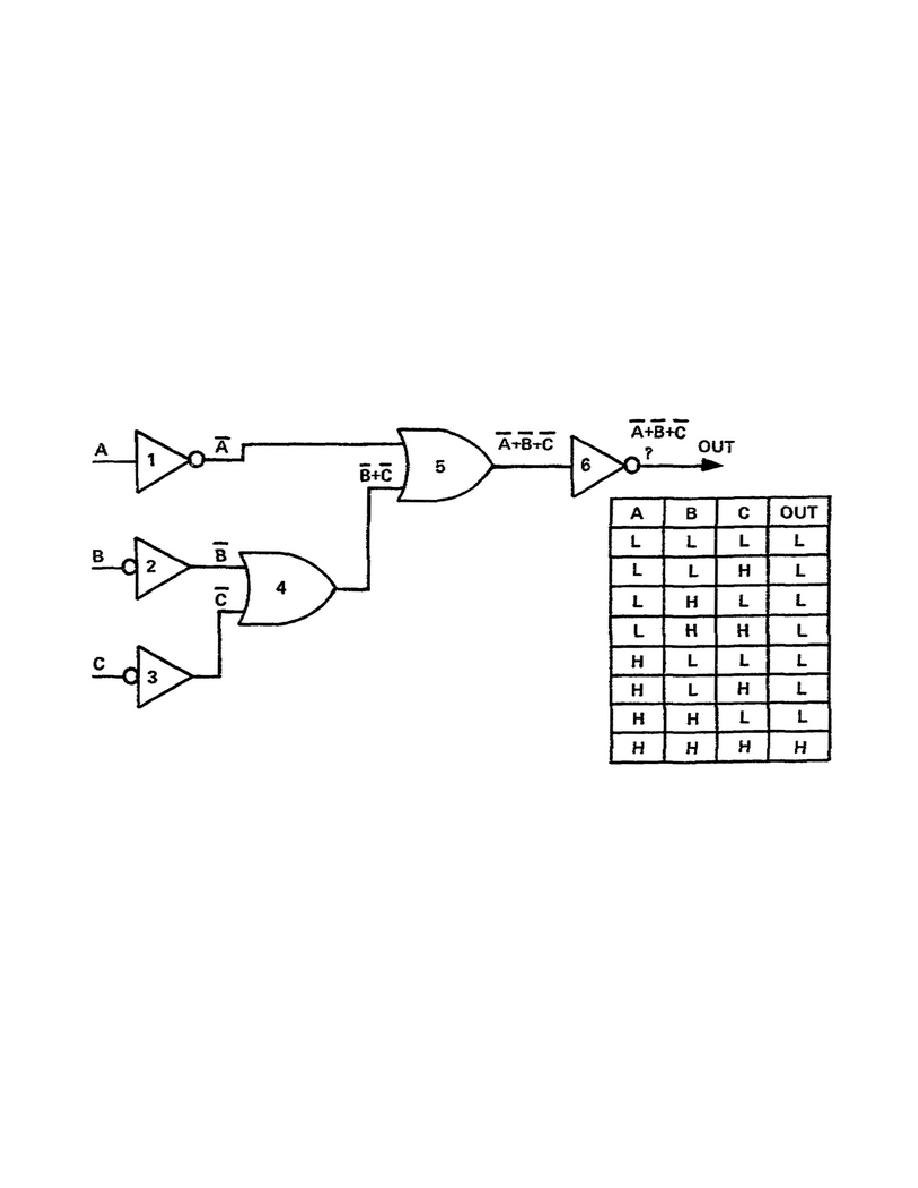
Look at the system in Figure 2-5 for an example. At first glance it appears to perform an OR
function of several inverted signals. If however, you use Boolean algebra, the system can be simplified
and proved to be performing an entirely different function. Simplify the final expression and what
remains? A 3-input AND function of ABC. The function is not at all what it first seems to be; the
function, at least for the output we are considering, represents an ANDing of the inputs.
Figure 2-5. A small system
3.
A truth table confirms our analysis of the function. The only input combination that enables the
circuit to produce a high output is when A, B, and C are all true (high). Trace each combination listed in
the truth table through the gates to be sure you understand the results.
4.
Normally, this circuit would not have been designed this way if only the ABC output was to be
used; a single AND circuit would have been used instead. However, peculiar arrangements of basic
circuits such as this one often occur within large logic diagrams, usually because other combinations of
the same input signals are required to satisfy other gates.
14




 Previous Page
Previous Page
