c. Seeing how formulas for db loss and
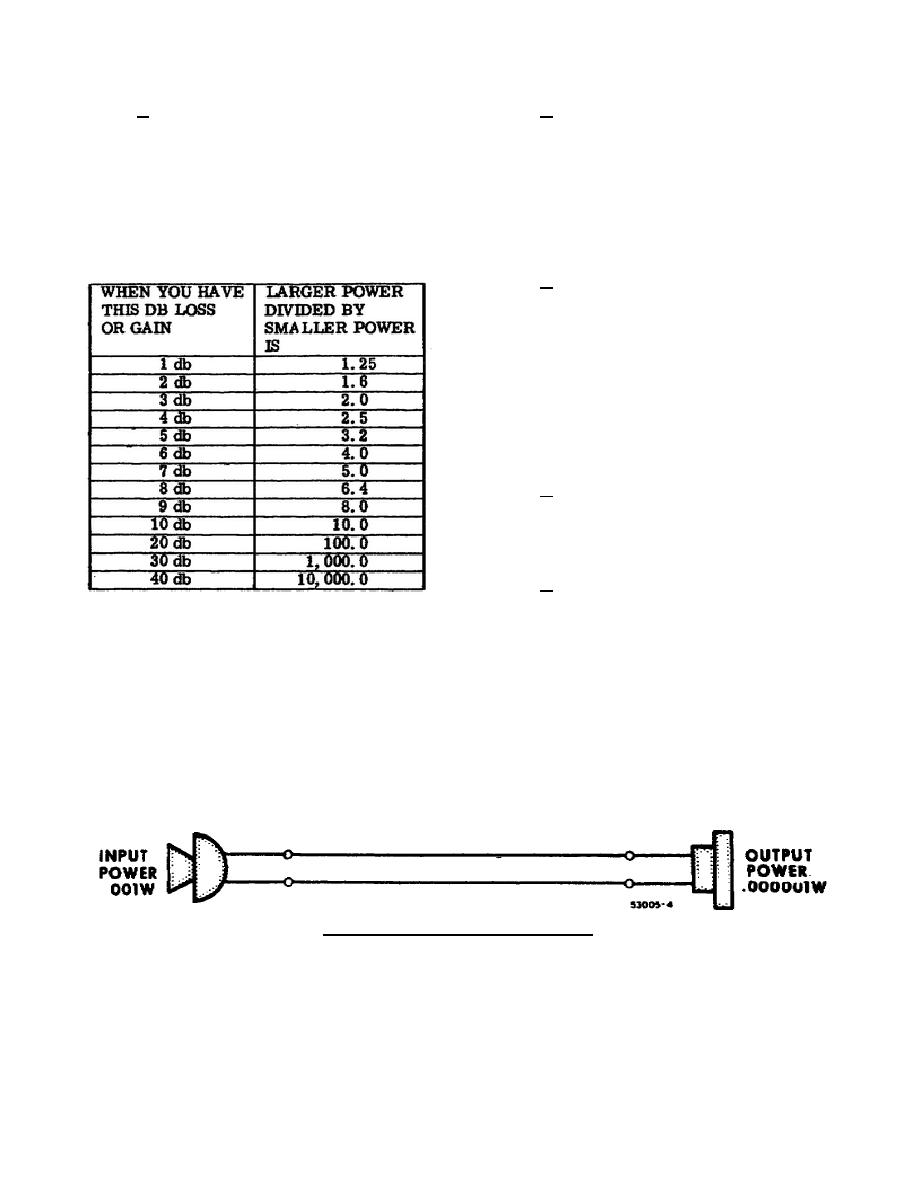
a. Example 1. Suppose you have a circuit
gain are solved has given you an idea of how db's
like that shown in figure 120 input power is .001
express the power ratio in a circuit. There is no need
watt and the output power is .000001 watt. The
to go into any further computations. Instead the
input power is greater than the output power so you
formula have been worked out for several common
have a power loss. To find the power loss, you
db losses and gains.
The results of these
divide .001 by .000001 which equals 1,000. In
computations are given in Table IV.
Table IV this corresponds to 30 db. So your answer
is: -30 db.
TABLE
b. Example 2. Suppose you know the db
gain is 40 db. The ratio of the output power to the
input power is found by referring to Table IV where
40 db corresponds to a ratio of 10,000. If you know
the input power is .001 watt, -you can find the
output power by multiplication: .001 watt x 10,000 =
10 watts.
4-24.
THE DBM REPRESENTS A REFERENCE
LEVEL
a. Before explaining the dbm, let's first
find out what is meant by a reference level. The
simplest way to explain it is to use an everyday
example.
b. Suppose you had 0 in a savings
account at the beginning of a year. This 0 could
act as a reference level. You could actually plot
4-23.
USING TABLE IV
your savings account for the whole year on a graph
as shown in figure 121. You'd put 0 in the center
You can find out how much power is lost or
of the vertical axis. And then place plus signs above
gained if you know the number of db's lost or
0 and minus signs below 0. Then as the year
gained. Or you can find out the number of db's lost
went on, if you deposited in February, you'd plot
or gained when you know the amount of power lost
+ (above 0). Then, if in March you had to
or gained. To show you how to use Table IV, here
withdraw you'd plot this to show that you had -
are a few examples.
(below 0). And as the year progressed you'd
plot the other months as shown.
Figure 120. Circuit showing power loss.
344 L4
153



 Previous Page
Previous Page
