point where the diagonals cross is the center of the rectangle or square.
This simple rule is invaluable, it enables you to solve problems that are
seemingly unsolvable.
Figure 3-2.
Division
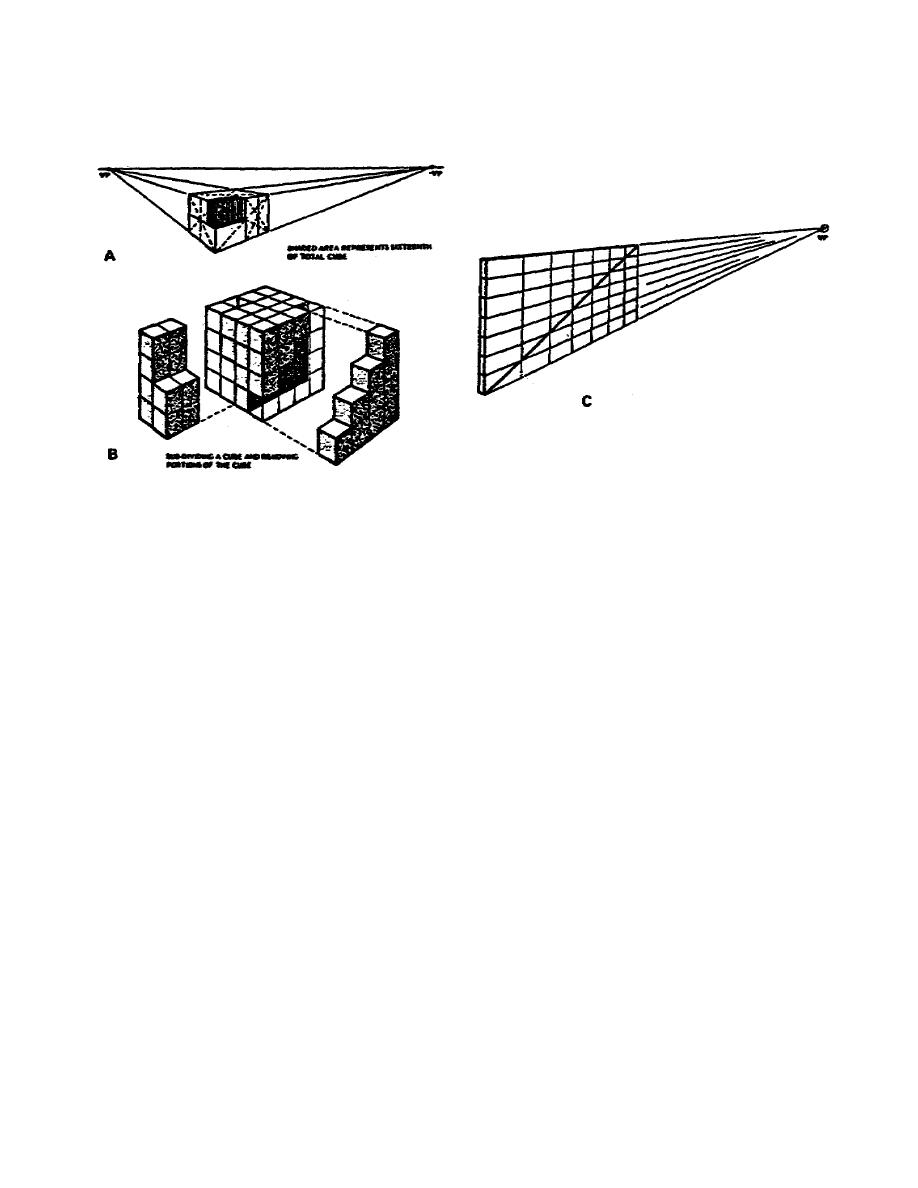
a. At other times it is necessary to divide an area, or a diagonal,
into a number of parts. Here a ruler alone will not suffice. As with most
division of space, the vertical (fig 3-2) or horizontal line (not shown)
parallel to the picture plane is the key. Aspect B of Figure 3-2 shows the
subdivision of a cube, portions removed. For example, to divide a receding
plane into any number of units, divide the left vertical height into the
desired number of parts with a ruler as shown in Figure 3-2.
Draw lines
from the points of division on the vertical line out to the vanishing point.
Then draw a line from corner to corner as shown, and the intersections of
the diagonal and the horizontal lines drawn to the vanishing point are the
correct points to add the other vertical lines.
b. Figure 3-3 shows the correct method of dividing a rectangular area
into uniform rectangular patterns, such as floor tiles.
The width of the
squares are first measured on a horizontal line (A). Two vanishing points
are established and lines are drawn from the divided horizontal line to the
left vanishing point, then the depth is established by drawing lines to the
right vanishing point.
A diagonal line is drawn from corner to corner,
points 1 and 2. Where the diagonal intersects the lines drawn to the left
vanishing point are-the correct points for the receding lines to be drawn to
the right vanishing point.
Notice that the lower drawing is a one-point
31



 Previous Page
Previous Page
