3. A diagonal drawn from the center point on the lower horizontal edge of
the square through the center point on the far edge will intersect the
extension of the top edge as shown in Figure 2-14. A vertical dropped from
this intersection will add the equivalent of a half to that side. As you
can see, this process can be continued as many times as necessary, and the
sections so established can be divided in turn.
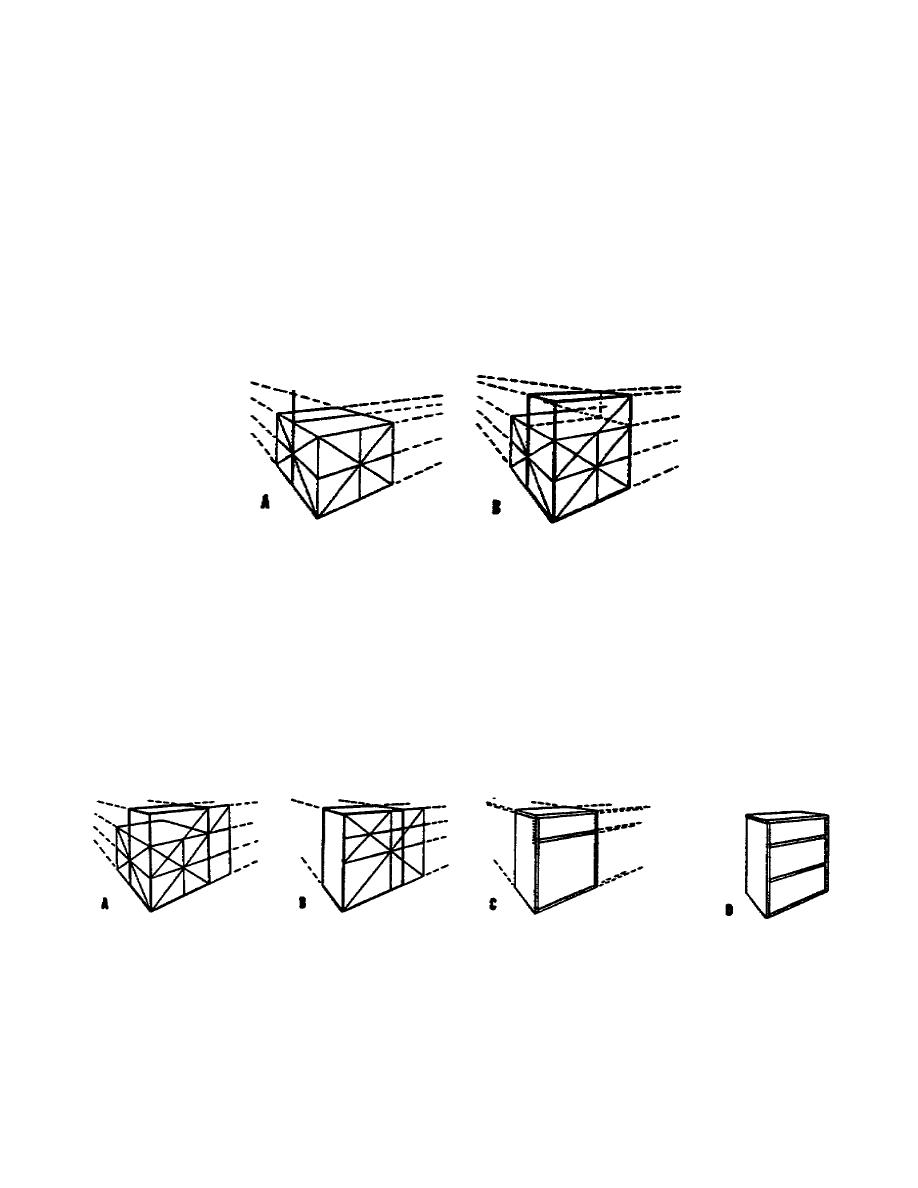
4. Now suppose you are asked to draw in perspective a bookcase 36 inches
high, 24 inches wide, and 12 inches deep.
Since the 36 inches can be
divided into 18 inches or 9 inches but not into 24 or 12, it will be better
to make the basic cube 24 inches, which can easily be divided into 12 inches
and to which 12 inches can be added. In Figure 2-15, these dimensions have
been established. Note that the same method used for multiplying areas in a
horizontal direction, shown in Figure 2-14, may be applied to multiplying
them in a vertical direction.
Figure 2-15. Finding the outside dimensions
of a bookcase in perspective.
5. Suppose that the bookcase is constructed of boards which are 1 inch
thick. The top shelf is 8 inches high; that is, the upper front edge is 9
inches from the top of the bookcase, and the lower shelves are 12 inches
high, that is, 13 inches including the width of one shelf, with the lowest 1
inch shelf resting on the floor. Notice that 9 inches is one-fourth of the
total height of the bookcase, which should make it easy to find this
dimension. A diagonal may be used to create a 36-inch square, as shown in
Figure 2-6, and diagonals may be used to locate the top shelf, as shown in
Figure 2-16.
Figure 2-16.
Locating the shelves of the bookcase
26



 Previous Page
Previous Page
