the segment. In this case, you add 32.5% and 25%, which equals 57.5%.
Continue plotting using the same procedure:
32.5% + 25.0% = 57.5% (the end of the second segment)
57.5% + 20.0% = 77.5% (the end of the third segment)
77.5% + 15.0% = 92.5% (the end of the fourth segment)
92.5% + 7.5% = 100.0% (the end of the fifth segment)
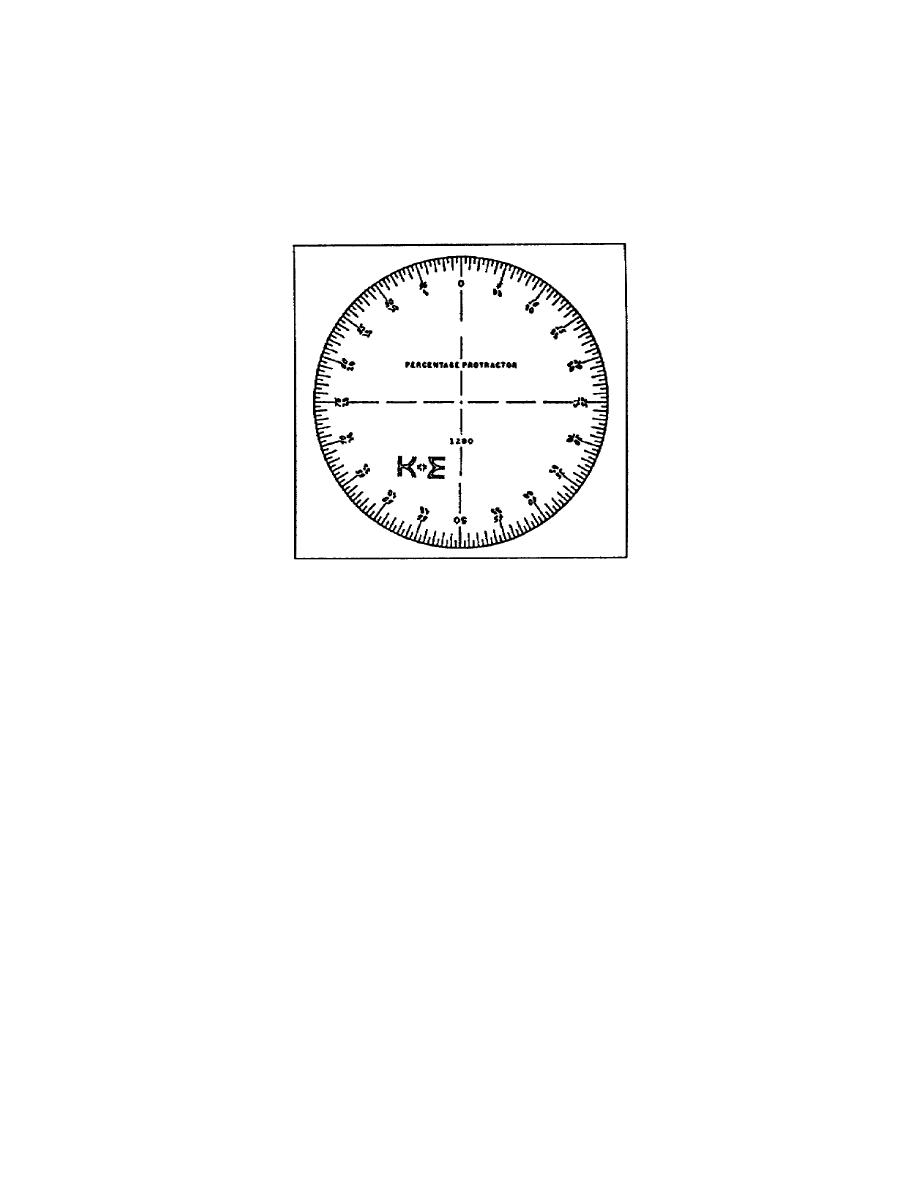
Figure 131. Percentage protractor
Before proceeding with the lesson, take a moment and review the plotting
procedure used with a percentage protractor. You placed the "0" percent
graduation at the 12 o'clock position (which placed the 50% graduation
at the 6 o'clock position). You plotted the largest segment first,
moving clockwise. The end of the first segment served as the start for
the second segment and so on. You plot the segments largest to smallest
moving clockwise. The proof that you plotted correctly was that the
last or smallest segment ended at the "0" percent graduation. You used
100% of the circle in your pie chart. If the last segment did not end
at the "0" percent graduation, you made a mistake, and you must recheck
your work.
(c) Plotting segments with a standard protractor. To plot the
segments using a standard protractor, you must determine the number of
degrees each segment uses. Before you can determine the number of
degrees each segment uses, you must determine how many degrees of the
circle makeup 1% of the circle. If you divide the total number of
degrees in a circle
1-37
SS0530



 Previous Page
Previous Page
